-
 Tennis: Djokovic senza età, in campo anche ad Adelaide
Tennis: Djokovic senza età, in campo anche ad Adelaide
-
Prezzo oro in calo, Spot scambiato a 4.279 dollari

-
 Tennis: Atp introduce norma anticalore, possibili stop agli incontri
Tennis: Atp introduce norma anticalore, possibili stop agli incontri
-
Psoriasi, 'anche in maternità soluzioni terapeutiche sicure ed efficaci'

-
 Borsa: l'Europa apre fiacca, Francoforte cede lo 0,4%
Borsa: l'Europa apre fiacca, Francoforte cede lo 0,4%
-
Prezzo petrolio in calo, Wti scambiato a 56,45 dollari

-
 Lo spread Btp-Bund apre invariato a 71 punti base
Lo spread Btp-Bund apre invariato a 71 punti base
-
Borsa: l'Asia pesante in attesa dei dati Usa, future in calo

-
 Euro poco mosso, scambiato a 1,1751 dollari
Euro poco mosso, scambiato a 1,1751 dollari
-
Forze armate russe abbattono un drone sui cieli di Mosca

-
 Usa colpiscono tre imbarcazioni nel Pacifico orientale, otto morti
Usa colpiscono tre imbarcazioni nel Pacifico orientale, otto morti
-
Zelensky, 'non riconosceremo il Donbass come territorio russo'

-
 Ft, gli Usa hanno sospeso l'accordo sulla tecnologia con il Regno Unito
Ft, gli Usa hanno sospeso l'accordo sulla tecnologia con il Regno Unito
-
Trump fa causa alla Bbc, chiede 5 miliardi

-
 1-0 al Como, la Roma rivede la vetta
1-0 al Como, la Roma rivede la vetta
-
In Venezuela i familiari chiedono la libertà dei prigionieri politici

-
 Trump, siamo più vicini che mai alla fine della guerra in Ucraina
Trump, siamo più vicini che mai alla fine della guerra in Ucraina
-
Europei e Usa, impegno per una forza multinazionale in Ucraina

-
 Leader europei, significativi progressi di Trump per la pace in Ucraina
Leader europei, significativi progressi di Trump per la pace in Ucraina
-
Ambasciatore d'Israele in Italia, 'qui gli ebrei non si sentono sicuri'

-
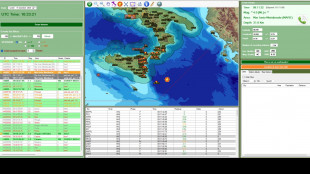 Terremoto 4.0 nel mar Ionio, rilevato da una stazione a 3,5 km di profondità
Terremoto 4.0 nel mar Ionio, rilevato da una stazione a 3,5 km di profondità
-
La cinese Cmoc acquista quattro miniere d'oro in Brasile

-
 iRobot getta la spugna, il robot aspirapolvere Roomba in bancarotta
iRobot getta la spugna, il robot aspirapolvere Roomba in bancarotta
-
Bozza Ue sull'automotive, 'maxi-incentivi per le mini car elettriche'

-
 Fincantieri, "la Fondazione ponte con la storia per costruire il futuro"
Fincantieri, "la Fondazione ponte con la storia per costruire il futuro"
-
Borsa: Milano maglia rosa in Europa, vola la Juve
-
 Merz, stasera Witkoff e Kushner ai colloqui con gli europei
Merz, stasera Witkoff e Kushner ai colloqui con gli europei
-
Kallas, rifiuto di Hamas a disarmo importante ostacolo alla pace

-
 Trump lancia la 'Tech Force', 1.000 ingegneri per l'IA
Trump lancia la 'Tech Force', 1.000 ingegneri per l'IA
-
Usa, risolto il 90% delle questioni tra Mosca e Kiev

-
 Lo spread Btp-Bund chiude in calo a 67 punti e torna a livelli 2008
Lo spread Btp-Bund chiude in calo a 67 punti e torna a livelli 2008
-
Eg Group completa la vendita delle attività, Esso torna italiana

-
 Il governo Milei denuncia la Federcalcio argentina per corruzione
Il governo Milei denuncia la Federcalcio argentina per corruzione
-
Usa, 'Trump soddisfatto del punto dei negoziati'

-
 'Io l'ho conosciuta', presentato il docufilm che racconta Mia Martini
'Io l'ho conosciuta', presentato il docufilm che racconta Mia Martini
-
Le cantate di Vivaldi secondo Raffaele Pe e La Lira di Orfeo

-
 Media, Reiner aveva in testa almeno un altro film
Media, Reiner aveva in testa almeno un altro film
-
Saline di Sicilia, parte il dossier per la candidatura al MaB Unesco

-
 Wall Street procede debole, Dj -0,06%, Nasdaq -0,07%
Wall Street procede debole, Dj -0,06%, Nasdaq -0,07%
-
Sciopero nazionale Coop per la cessione di 24 punti vendita del Centro Italia

-
 Zelensky, i colloqui con gli Usa non facili ma molto produttivi
Zelensky, i colloqui con gli Usa non facili ma molto produttivi
-
Un rene ad una sconosciuta, decima donazione samaritana in 10 anni
-
 Apparecchi medici medio-piccoli troppo vecchi, 50% rinnovato solo dopo 10 anni
Apparecchi medici medio-piccoli troppo vecchi, 50% rinnovato solo dopo 10 anni
-
Rientra in Italia dagli Usa e porta un'azienda di tecnologie quantistiche

-
 Slittano i tempi della manovra, la capigruppo deciderà il calendario
Slittano i tempi della manovra, la capigruppo deciderà il calendario
-
Antartide occidentale, dallo scioglimento dei ghiacci mari più alti di 5 metri

-
 Trovate microplastiche anche nell'unico insetto autoctono dell'Antartide
Trovate microplastiche anche nell'unico insetto autoctono dell'Antartide
-
Manovra: arriva il gioco 'Win for Italia Team', parte delle risorse al Coni

-
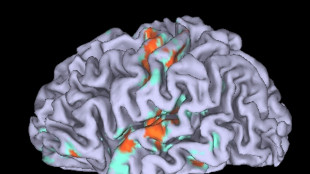 Il cancro interrompe il ritmo naturale del cervello, causa insonnia e ansia
Il cancro interrompe il ritmo naturale del cervello, causa insonnia e ansia
-
Borsa: l'Europa riduce il rialzo con Wall Street in calo

Enigma occhi blu svelato
Un enigma logico che ha catturato l'attenzione di appassionati di matematica e logica in tutto il mondo è noto come "L'indovinello degli isolani dagli occhi blu e marroni". Questo rompicapo, caratterizzato da una premessa intrigante e una soluzione sorprendente, si basa su un principio fondamentale della matematica: l'induzione. La sua popolarità è cresciuta negli ultimi anni, grazie alla diffusione online di problemi logici che sfidano il ragionamento umano e mettono alla prova la capacità di deduzione.
La premessa dell'indovinello
Immaginiamo un'isola remota abitata da 1000 persone: 100 con gli occhi blu e 900 con gli occhi marroni. Su quest'isola vige una regola sociale tanto curiosa quanto rigida: nessuno deve conoscere il colore dei propri occhi. Se un isolano scopre il proprio colore, è obbligato a lasciare l'isola il mattino seguente. Per garantire che ciò non accada, non esistono specchi, l'acqua è conservata in contenitori opachi e parlare del colore degli occhi è assolutamente proibito. Gli isolani, tuttavia, sono dotati di un'intelligenza straordinaria e di una capacità di ragionamento logico impeccabile.
Un giorno, un viaggiatore giunge sull'isola e, durante un banchetto, pronuncia una frase apparentemente innocua: "Che bello! Vedo almeno una persona con gli occhi blu!" Questa semplice affermazione innesca una reazione a catena che, dopo esattamente 100 giorni, porta tutti i 100 isolani con gli occhi blu a lasciare l'isola.
La soluzione: il potere dell'induzione matematica
Per comprendere come ciò avvenga, dobbiamo ricorrere all'induzione matematica, un metodo che permette di dimostrare una proprietà per un numero infinito di casi partendo da un esempio base e procedendo passo dopo passo.
Caso base: un solo isolano con gli occhi blu
Se sull'isola ci fosse una sola persona con gli occhi blu, questa si troverebbe in una situazione unica. Non vedendo nessun altro con gli occhi blu, e sentendo l'affermazione del viaggiatore ("Vedo almeno una persona con gli occhi blu"), capirebbe immediatamente di essere lei stessa quella persona. Di conseguenza, lascerebbe l'isola il mattino successivo, cioè dopo 1 giorno.
Passo induttivo: da n a n+1
Supponiamo ora che la regola valga per un numero n di isolani con gli occhi blu: se ci sono n persone con gli occhi blu, tutte lasceranno l'isola dopo esattamente n giorni. Consideriamo cosa accade se ci sono n+1 isolani con gli occhi blu.
Ogni isolano con gli occhi blu vede n persone con gli occhi blu intorno a sé. Ognuno pensa: "Se io non avessi gli occhi blu, ci sarebbero solo n persone con gli occhi blu, e queste, secondo la regola, lascerebbero l'isola dopo n giorni." Tuttavia, se dopo n giorni nessuno lascia l'isola, ogni isolano con gli occhi blu si rende conto che il numero di persone con gli occhi blu deve essere superiore a n. Dato che vede solo n persone con gli occhi blu, deduce che anche lui deve avere gli occhi blu. Così, tutti gli n+1 isolani con gli occhi blu arrivano alla stessa conclusione e lasciano l'isola insieme il mattino seguente, dopo n+1 giorni.
Il caso specifico: 100 isolani con gli occhi blu
Applichiamo ora questo ragionamento al caso dell'isola con 100 isolani con gli occhi blu. Il primo giorno, ogni isolano con gli occhi blu vede 99 persone con gli occhi blu e aspetta che, se fossero solo 99, queste lasciassero l'isola dopo 99 giorni. Ma quando il 99esimo giorno passa senza che nessuno parta, tutti capiscono che il numero di isolani con gli occhi blu deve essere almeno 100. Al 100esimo giorno, quindi, i 100 isolani con gli occhi blu deducono il proprio colore e lasciano l'isola insieme.
Il ruolo cruciale del viaggiatore
L'affermazione del viaggiatore non rivela nulla di nuovo in senso stretto: ogni isolano con gli occhi marroni vede almeno 100 persone con gli occhi blu, e ogni isolano con gli occhi blu ne vede almeno 99. Tuttavia, ciò che cambia è che questa informazione diventa "conoscenza comune". Prima dell'arrivo del viaggiatore, nessuno poteva essere certo di cosa gli altri sapessero o pensassero. Con la sua dichiarazione, tutti sanno che tutti sanno che c'è almeno una persona con gli occhi blu, e questo avvia il processo di deduzione logica che culmina dopo 100 giorni.
Conclusione: un enigma che illumina la logica
L'indovinello degli isolani dagli occhi blu e marroni non è solo un passatempo intrigante, ma una dimostrazione elegante di come la logica e l'induzione matematica possano risolvere problemi apparentemente impossibili. La sua soluzione sottolinea l'importanza della conoscenza condivisa e del ragionamento collettivo, offrendo uno spunto di riflessione per chi ama esplorare i confini della mente umana. Questo rompicapo continua a essere discusso e analizzato, mantenendo viva la curiosità di chi si cimenta con le sue sottili sfumature logiche.

Zelenskyy: “Israele e Ucraina, qual è la differenza?”

UE-Ungheria: Causa per la legge sulla «sovranità»

Asse Scholz-Macron: accordi e anche attriti...

Ucraina: Zelensky chiede aiuto internazionale

Bruxelles, la protesta dei "lavoratori essenziali"

NATO: l'Ucraina è “in cima alla lista”!

Francia: Michel Barnier chiede “compromessi”

Bielorussia: CPI indaga sul dittatore Lukashenko

UE: Google presenta una denuncia contro Microsoft

NATO si addestra a combattere gli attacchi informatici

Gemello dell'Oceano Digitale: Proteggere gli Oceani



